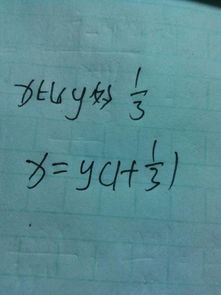
几又几分之几：探究数学中的无限小与无穷大 在数学中，分数是一种重要的表达方式。而无限小和无穷大则是分数的两个极端值。它们在数学中有着重要的应用，同时也是无限数学中的两个重要概念。本文将带您了解无限小与无穷大的概念及其在数学中的应用。 1. 无限小 无限小是指一个数趋近于零时的简化形式。例如，1/3 就可以表示为 0.3333...，它无限接近于零但永远不会等于零。无限小可以看作是分数中的“0”部分。它们在数学中有着广泛的应用，尤其是在极限和级数等领域。 2. 无穷大 无穷大是指一个数趋近于正无穷或负无穷时的简化形式。例如，1/2 就可以表示为 0.5，它无限接近于正无穷但永远不会等于正无穷。无穷大可以看作是分数中的“∞”部分。它们在数学中也有着广泛的应用，尤其是在极限和级数等领域。 3. 无限小与无穷大的关系 无限小和无穷大是分数的两个极端值，它们之间的关系在数学中有着重要的意义。例如，在求解无限大的问题时，常常需要使用无限小的近似值来逼近无限大的值。同时，在求解无限小的问题时，也需要使用无限大的近似值来逼近无限小的值。 4. 无限小与无穷大的应用 无限小和无穷大在数学中有着广泛的应用。例如，它们在求解极限和级数问题时起着重要的作用。此外，它们还在微积分、概率论和统计学等领域有着重要的应用。 总之，无限小和无穷大是分数的两个重要概念，它们在数学中有着广泛的应用。了解它们的概念和应用将有助于您更深入地理解数学。